October 5, 2021 | Dukus | 17 Comments
So I rewrote big parts of the user interface for the game. Why? As I've been adding features to the simulation for the new game, I've needed to display more and more interface elements on the screen. As I was adding them, I was constantly reminded that I'm not really satisfied with big parts of the way the user interface. The user interface I had previously written worked fine. But it took a ton of work and code to create, change and modify things once they were in place. Restyling or reorganizing layouts was labor intensive, and adding new functionality took a lot of C++. So I'm trying to do less busy work this time. I've changed the internals to make me more productive, I've also worked on some nicer user facing features as well. So whats first? In Banished, of the C++ game level code, 20% of the code was for the user interface. It was event driven and it piled up quick. For anything that I wanted to have user controlled or displayed, I wrote a chunk of code that searched for controls in data files, connected to them, decided if they were enabled or disabled, visible or invisible, what they should display, and what happened when each control received events.Too much C++ code.
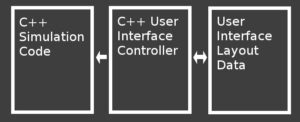
The way it was set up, if I wanted to change the layout of the user interface, or change what sort of control was used, I had to change the layout data, and the ui code. If I didn't keep them in sync, the game wouldn't work, or it might crash. I don't like such tight coupling between code and data, and wanted to get rid of it.
And so I switched to a data binding setup instead. It cuts out the middle man, and controls just work directly on data.
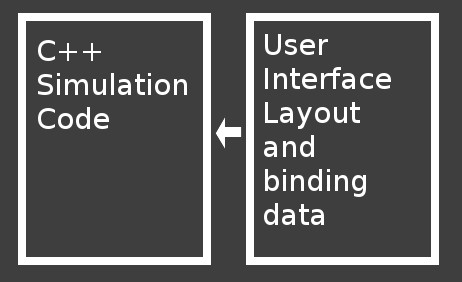
Any data in the engine also can carry attributes that go along with it, such as valid ranges for numbers and if you can interact with it. I can also bind a control to a function in code, so that on a button press, a function in the c++ is called directly, rather than having some in-between code. Or it can do both, when you change a number in the user interface, it changes the value, and calls a function to let the code know something changed.
This gives me a lot of flexibility. I can change a control from a simple displayed number, to an edit box, to a progress bar, to a drop down with options, all working on the same single value in the game. No code change required, just data that points to the value. It can also take lists of values (or anything else, like text or complex structures) and populate controls automatically.
The game code no longer cares about the display of data or how it's presented. It can even connect multiple controls to a single piece of data. A progress bar could show a value and how big or small the value could be and at the same time another control could change the value - both will update and require no additional C++ code.
As an example, to set the image on a button, and call a function when pressed, the data now looks something like this:
Button(_binding = "Image: _entity.MetaData._sprite, Control: _entity.Interact.Disable")
And that's it. As long as the object the UI is controlling has a MetaData component and an Interact component everything is fine. If they don't the control just doesn't do anything. No crashes, no extra C++ code, it just works.
To show how much more data driven and shorter the new way is, here's some pseudocode of the old C++ method I used to use.
void Dialog::UIInit()
{
Element* button = dialog->FindButton("disableButton");
_Assert(button != nullptr); // broken if can't find button in the data!
button->SetElementId(DisableButton_Id);
_Assert(_entity->GetMetaData() != nullptr); // does this entity actually have this?
button->SetSprite(_entity->GetMetaData()->_sprite);
}
void Dialog::UIEvent(int32 eventId, int32 elementId)
{
if (eventId == UI::ButtonPressed && elementId == DisableButton_Id)
{
_Assert(_entity->GetInteract() != nullptr); // another validity check
_entity->GetInteract()->Disable();
}
}
So imagine a user interface with 10 different controls on it and how big the C++ gets...
One tricky thing about this method is when I need data that isn't directly available in the simulation. For example, under the hood, I never need to keep a list of inventory sorted by name, but when displayed on screen it might need to be so. So the only C++ UI code I write now is a small chunk to prepare data that can be bound when the user interface is displayed. So it actually is like this:
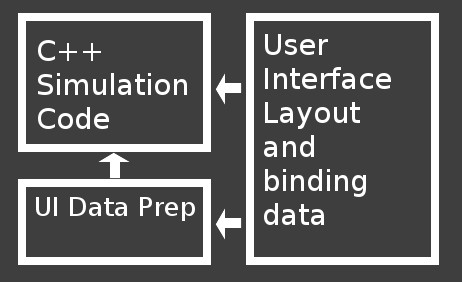
Another cool thing is that this new method of using the user interface was just an addition. The old method is still there - so in the case that I need to manually handle the controls on an interface, do something complicated, or build user interface completely from code, I can.
This has gotten a bit long, so next time i'll talk about how I made designing and laying out interface elements a bit easier.
This is all super interesting. Not too long at all! I used to be a computer programmer many years ago and still find it interesting to read about - and of course, LOVE Banished - thousands of hours invested. Lol.
Thanks for your hard work, enjoying learning about this project!
Been there since 2012 and still love to read you.
I believe you are a millionaire and still find passion about making games.
Love it, true values.
Thanks for your hard work m8, loved this game, hope some day we will see Banished 2
Congratulations, you just invented MVC 🙂
The next part of course is, how does the control know when the data point it's bound to has been changed and thus needs to refresh itself?
I was so happy to find a new update from you. The UI in the Banished felt great, hence I am really looking forward to the improved next generation and your next blog about it. I hope we could see some examples.
I wish you all the best!
@Jared. There are no pointers to actual fields stored - there's a polling mechanism and data exchange that occurs every update. So values are always up to date and the controls are built to handle changes.
"This is a city building game I've been working on for a while, it's called Banished. And I'm gonna show you how to start a new town. I have some resources I collected for construction as well as some food and firewood the people need to stay warm and eat. I'm gonna need to produce some more food, so the first thing I'm gonna do is make a crop field.... " - Luke. March 20, 2013.
A lot has happened in 8.5 years, but its been a great journey thus far.
I look forward to the future along with everyone else that you've impacted .
Thanks man !
-jasonrubik
Love the game, love the updates!
All I know of coding is how to change a font in html, but I love Banished so much that I still skimmed through this, and even found it interesting. Keep it up!
Very cool! Sounds like it will streamline your work quite a bit!
Ducus
This is eating away at my level of anticipation, not in the sense that it is waning, but rather increasing it LOL.
if this game is anything like Banished in terms of gam play, it is bound to become yet another massive epic from Shining Rock.
My prayer is that you do not compromise on your unique game play programming. I now have tried and bought many other city builders in the same category, only to be seriously disappointed in their gameplay options/programming.
Perhaps I'm a little (LOL, A LOT) Banished biased, but have yet to find a game that is as user friendly and brilliantly constructed with a flexible UI to die for that does everything possible to help you fully control your game.
Can't wait for this new game and good luck with tons of God speed
Piet
I hope this game will be Banished II. Still playing Banished to this day. I do use Mods made for it too. I'm part of the Civ IV BtS Mod Caveman2Cosmos team. I don't program I do game play balance.
Any way Keep up the Good work and God Bless! 😀
I know absolutely nothing about programming but always enjoy the time taken to post about it.
Really enjoy these tech articles ... and recruiting people to play Banished!
Keep up the good work, and we're all looking forward to your next project!
-John
One thing in particular stands out to me from your work.
You actually finished.
You imagined a game, and you built it. And when you felt you were done, you stopped.
I love that. Too often in modern development creep sets in and before you know it the core vision is lost.
Big kudos to you for just letting it finish.
Best of luck for your current endeavour. When it’s available, I’ll buy it :)!
That was interesting as alway. I actually found it easy to read, not too long at all.
As someone who's been reading these for years, still very interesting to get a well written sneak peak behind the hood 🙂 Thanks